灰狼属于犬科动物,被认为是顶级的掠食者,它们处于生物圈食物链的顶端。灰狼大多喜欢群居,每个群体中平均有5至12只狼。灰狼群体有着严格的社会等级制度,如图1所示,其中α是狼群的领导者,负责所有决策;β协助α进行决策,必要时进行接替,地位仅次于α;δ则服从于α和β,负责放哨、侦察等事务;ω处于社会底层,是不可缺少的普通狼,负责种群内部关系的平衡。
图1:灰狼的等级制度,引用自论文《Grey Wolf Optimizer》
集体狩猎是灰狼的一种社会行为,社会等级在集体狩猎过程中发挥着重要的作用,捕食的过程在α的带领下完成。主要包括三个步骤:1)跟踪和接近猎物;2)骚扰、追捕和包围猎物,直到它停止移动;3)攻击猎物。灰狼的集体狩猎行为如图2所示。
图2:灰狼集体狩猎行为,引用自论文《Grey Wolf Optimizer》
灰狼优化算法的主要思路是假设α、β、δ更了解猎物的潜在位置,即优化问题的决策空间中最佳解决方案所在的位置,其他灰狼个体依据α、β、δ的位置来更新其自身位置,逐渐逼近猎物(最优解)。算法直接将前3匹适应度最高的狼分别定义为α,β和δ,它们指导其他狼向着目标搜索。在狩猎过程中,灰狼的基本位置更新方式定义为:
D ⃗ = ∣ C ⃗ ⋅ X p ⃗ ( t ) − X ⃗ ( t ) ∣ (1) \vec{D}=|\vec{C}\cdot\vec{X_p}(t)-\vec{X}(t)|\tag1
D = ∣ C ⋅ X p ( t ) − X ( t ) ∣ ( 1 )
X ⃗ ( t + 1 ) = X p ⃗ ( t ) − A ⃗ ⋅ D ⃗ (2) \vec{X}(t+1)=\vec{X_p}(t)-\vec{A}\cdot\vec{D}\tag2
X ( t + 1 ) = X p ( t ) − A ⋅ D ( 2 )
式(1)计算个体与目标间的距离,式(2)是灰狼的位置更新公式。其中,X ⃗ \vec{X} X D ⃗ \vec{D} D A ⃗ \vec{A} A C ⃗ \vec{C} C
A ⃗ = 2 a ⃗ ⋅ r 1 ⃗ − a ⃗ (3) \vec{A}=2\vec{a}\cdot\vec{r_1}-\vec{a}\tag3
A = 2 a ⋅ r 1 − a ( 3 )
C ⃗ = 2 r 2 ⃗ (4) \vec{C}=2\vec{r_2}\tag4
C = 2 r 2 ( 4 )
其中,a ⃗ \vec{a} a r 1 ⃗ \vec{r_1} r 1 r 2 ⃗ \vec{r_2} r 2
在模拟灰狼进行狩猎时,根据当前三个最优解所在的位置更新所有搜索单元的位置。灰狼集体狩猎时的行为定义如下:
{ D α ⃗ = ∣ C 1 ⃗ ⋅ X α ⃗ − X ⃗ ∣ D β ⃗ = ∣ C 2 ⃗ ⋅ X β ⃗ − X ⃗ ∣ D δ ⃗ = ∣ C 3 ⃗ ⋅ X δ ⃗ − X ⃗ ∣ (5) \left\{
\begin{array}{l}
\vec{D_α}=|\vec{C_1}\cdot\vec{X_α}-\vec{X}| \\
\vec{D_β}=|\vec{C_2}\cdot\vec{X_β}-\vec{X}| \\
\vec{D_δ}=|\vec{C_3}\cdot\vec{X_δ}-\vec{X}|
\end{array}
\right.
\tag5
⎩ ⎨ ⎧ D α = ∣ C 1 ⋅ X α − X ∣ D β = ∣ C 2 ⋅ X β − X ∣ D δ = ∣ C 3 ⋅ X δ − X ∣ ( 5 )
{ X 1 ⃗ = X α ⃗ − A 1 ⃗ ⋅ D α ⃗ X 2 ⃗ = X β ⃗ − A 2 ⃗ ⋅ D β ⃗ X 3 ⃗ = X δ ⃗ − A 3 ⃗ ⋅ D δ ⃗ (6) \left\{
\begin{array}{l}
\vec{X_1}=\vec{X_α}-\vec{A_1}\cdot\vec{D_α} \\
\vec{X_2}=\vec{X_β}-\vec{A_2}\cdot\vec{D_β} \\
\vec{X_3}=\vec{X_δ}-\vec{A_3}\cdot\vec{D_δ}
\end{array}
\right.
\tag6
⎩ ⎨ ⎧ X 1 = X α − A 1 ⋅ D α X 2 = X β − A 2 ⋅ D β X 3 = X δ − A 3 ⋅ D δ ( 6 )
X ⃗ ( t + 1 ) = X 1 ⃗ + X 2 ⃗ + X 3 ⃗ 3 (7) \vec{X}(t+1)=\frac{\vec{X_1}+\vec{X_2}+\vec{X_3}}{3}\tag7
X ( t + 1 ) = 3 X 1 + X 2 + X 3 ( 7 )
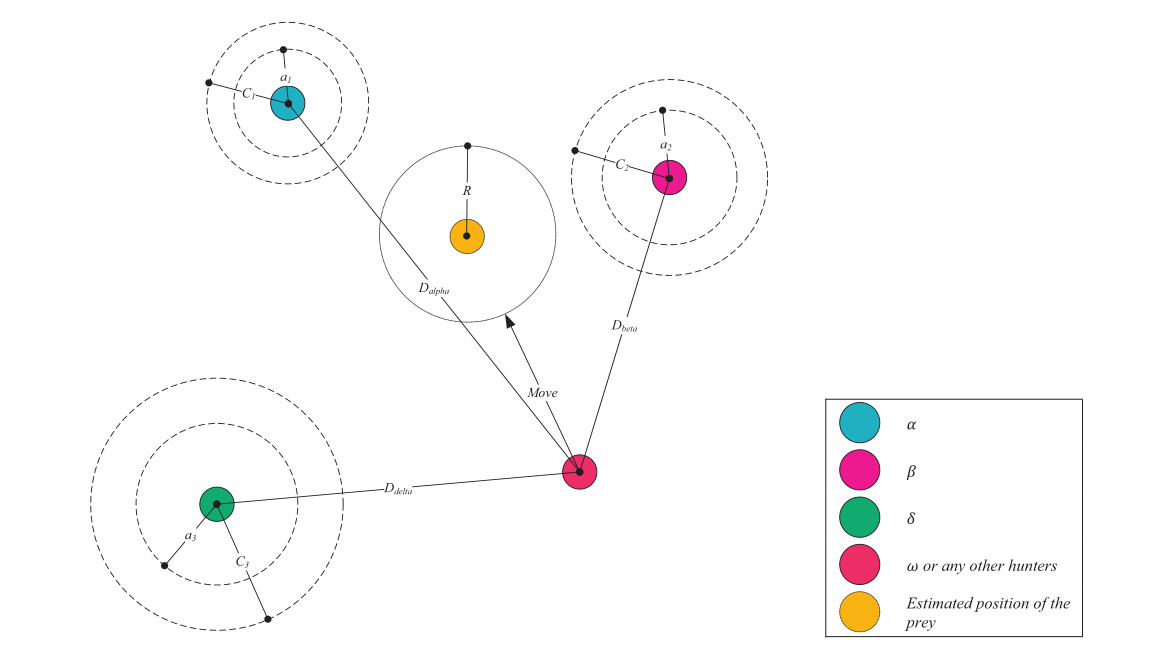
其中D α ⃗ \vec{D_α} D α D β ⃗ \vec{D_β} D β D δ ⃗ \vec{D_δ} D δ X α ⃗ \vec{X_α} X α X β ⃗ \vec{X_β} X β X δ ⃗ \vec{X_δ} X δ X ⃗ \vec{X} X X ⃗ ( t + 1 ) \vec{X}(t+1) X ( t + 1 ) A ⃗ \vec{A} A C ⃗ \vec{C} C ∣ A ∣ ⃗ \vec{|A|} ∣ A ∣ ∣ A ∣ ⃗ \vec{|A|} ∣ A ∣ D ⃗ \vec{D} D C ⃗ \vec{C} C X ⃗ \vec{X} X
图3:灰狼位置更新示意图,引用自论文《Grey Wolf Optimizer》
灰狼优化算法的伪代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 初始化灰狼种群 Xi (i=1,2,…,n) 初始化 a, A, C 计算每个搜索单元的适应度 Xα=最优搜索单元 Xβ=第二优搜索单元 Xδ=第三优搜索单元 while (t<最大迭代次数) for (每个搜索单元) 根据公式2.7更新当前搜索单元的位置 end for 更新a, A, C 计算所有搜索单元的适应度 更新Xα,Xβ,Xδ t=t+1 end while return Xα